
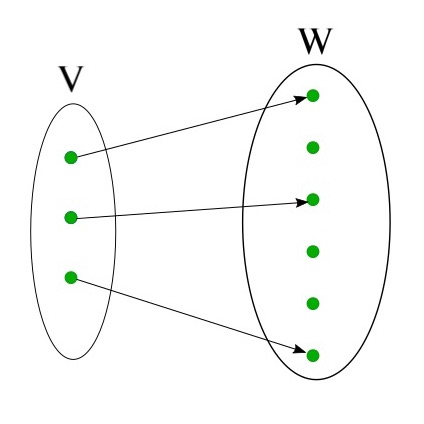
In each part, V and W are finite-dimensional vector spaces (over F ), and T is a function from V to W. Each module is designed to help a linear algebra student learn and practice a. 1.Label the following statements as true or false. Since $X$ is compact, there is a convergent subsequence $\(x)=1. Friedberg, Fourth Edition (Chapter 2) 2019. a) Prove that a linear map T is 1-1 if and only if T sends linearly independent sets to linearly independent sets. Suppose that T: V W is a linear map of vector spaces. If it does, the graph is not one-to-one and if it only intersects at one point, it will be one-to-one. Let $(x,y)\in X\times X$, and consider the sequence $(f^k(x),f^k(y))$. Call a subset S of a vector space V a spanning set if Span(S) V.
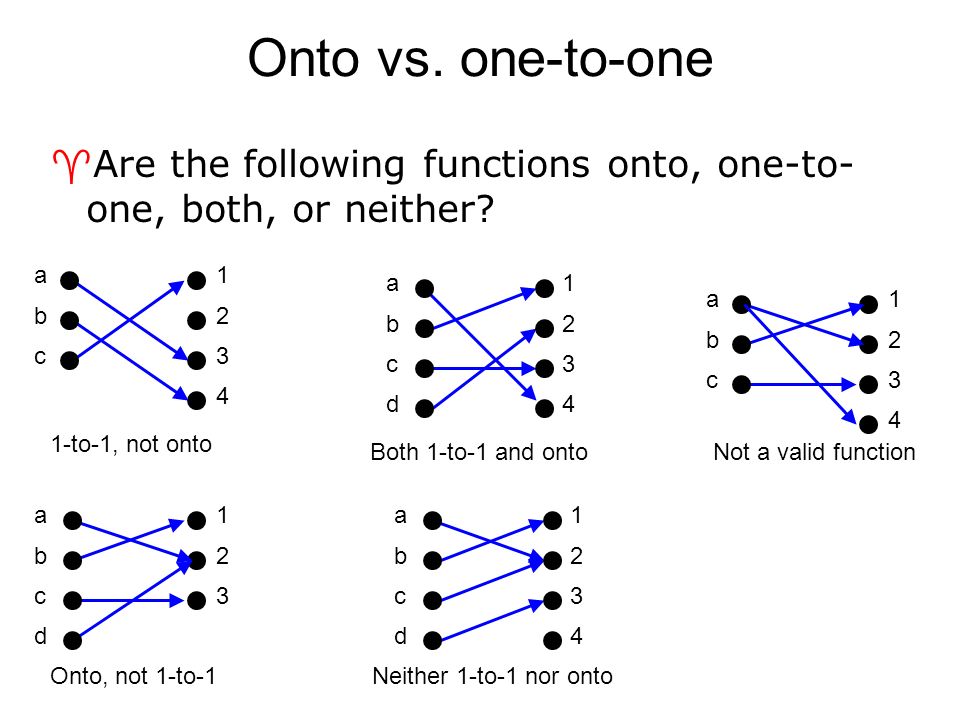
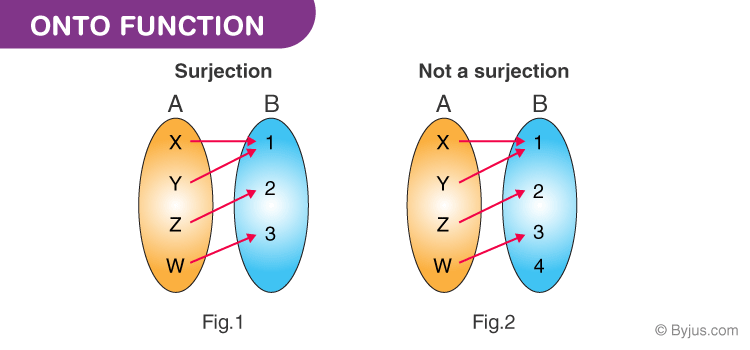
A mapping $f$ as above must be an isometry. A function is one-to-one if any two different inputs in the domain correspond to two different outputs in the range.That is, if and are two different in-puts of a function then Put another way, a function is one-to-one if no y in the range is the image of more than one x in the domain. The proof I came up with long ago consists of two lemmas. give functions such as the one in Figure 6 a special name. Let $(X,d)$ be a compact metric space, and assume that the mapping $f\colon X\to X$ does not decrease distances, that is $d(f(x),f(y))\ge d(x,y)$ for all $x,y\in X$. Then there exist v 1 v n2Sand some not all zero scalars a 1 a n such that a 1T(v 1) + + a nT(v n) 0: Since Tis. We want to show that T(S) is linearly independent. Let Sbe a linearly independent subset of V. It gives the orthogonal projection of point (x, y) onto the x-axis. V onto linearly independent subsets of W. There is an improvement of the answer of Joseph Van Name which I feel is much more in the spirit in the question asked: One can say that to each matrix A there corresponds a linear transformation T : Rn.


 0 kommentar(er)
0 kommentar(er)
